


Next: Evaluating the Jacobian matrix analytically
Up: Splice and template files
Previous: Extension to non-autonomous Hamiltonian systems
As another practical example of the use of the template file approach,
consider writing a general program for solving a system of equations of
the form:
| 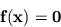 |
(2) |
using Newton's method [32]. A bold typeface is again used to
denote a vector.
The system of iterates can be written as:
| 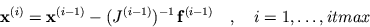 |
(3) |
where 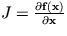 denotes the
Jacobian matrix and
denotes the
Jacobian matrix and 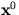 is a given set of initial values used to start
the iteration process. (Jk)-1 denotes the inverse of J(k) and the
superscript k denotes evaluation at iterate
is a given set of initial values used to start
the iteration process. (Jk)-1 denotes the inverse of J(k) and the
superscript k denotes evaluation at iterate 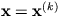 . The
iterative process is continued until some stopping criteria are satisfied at
iteration
itmax. When the system to be solved is scalar valued, (Jk)-1 is
simply the reciprocal of Jk. For practical implementation,
(3) is rewritten at each iteration as:
. The
iterative process is continued until some stopping criteria are satisfied at
iteration
itmax. When the system to be solved is scalar valued, (Jk)-1 is
simply the reciprocal of Jk. For practical implementation,
(3) is rewritten at each iteration as:
| 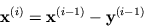 |
(4) |
where 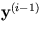 satisfies
satisfies
| 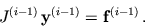 |
(5) |
The linear system (5) is typically
solved using LU decomposition of the Jacobian matrix at each iteration. The
value of 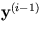 thus obtained is substituted into (4)
to obtain
thus obtained is substituted into (4)
to obtain 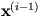 .
.



Next: Evaluating the Jacobian matrix analytically
Up: Splice and template files
Previous: Extension to non-autonomous Hamiltonian systems
Jorge Romao
5/14/1998
![]()
![]()
![]()
![]()