Optimising the code

 Computationally, the most expensive part in evaluating the function subroutine comes from the computation of the derivative of the potential term:

$${{\partial V({\bf q})} \over {\partial q_i}} = {q_i \over \sqrt{(q_1^2+q_2^2+q_3^2)}} \quad,\quad i=1,\ldots,3$$

In particular, evaluation of the fractional power is common to all components. This problem is found in many areas of molecular dynamics simulations ($-\nabla_{\bf q} V({\bf q})$ is analogous to the force).

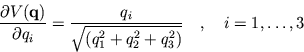
Common sub-expressions can be extracted using Mathematica's pattern matching rules before code translation is performed - in an attempt to optimize the resulting FORTRAN code. In general any structural knowledge of the problem in hand should been used to optimize the code. However, some computer algebra systems often use syntactic optimization to extract common sub-expressions and factor powers. The option AssignOptimize makes use of the package Optimize.m to automatically produce an optimized computational sequence, as outlined in section 5. The user is encouraged to try the optimization option on the example of the previous section. For example, after loading the optimization package, the following statement produces an optimized sequence for the problem.

FortranAssign[
    f, 
    Flatten[{Outer[D,{H},pvars],- Outer[D,{H},qvars]}],
    AssignOptimize->True,AssignToArray->{p,q},
    OptimizeNull->{p,q},OptimizePower->Binary
]

The option OptimizeNull effectively tells the optimization procedure that p and q are arrays (and not functions) and should not be considered as candidates for optimization. The option OptimizePower is used to binary factor powers, which has the added benefit of making use of the efficient FORTRAN intrinsic sqrt. The resulting output is given below.

        o1=q(1)**2
        o2=q(2)**2
        o3=q(3)**2
        o4=o1+o2+o3
        o5=sqrt(o4)
        o6=o4*o5
        o7=1/o6
        f(1)=p(1)
        f(2)=p(2)
        f(3)=p(3)
        f(4)=o7*q(1)
        f(5)=o7*q(2)
        f(6)=o7*q(3)

In practice, better numerical schemes exist for Hamiltonian systems than the standard explicit 4th order Runge-Kutta method [25].